Bunlar 15° 75° 90° üçgeni, 30° 60° 90° üçgeni ve 15° 15° 150° üçgenidir Bu üçgende 15°'lik açının karşısındaki kenar 1 birim ise 75°'lik kenarın karşısındaki kenar 2 √3 birim olur İspatı ise 22,5° 67,5° 90° üçgeninde olduğu gibidir Yalnızca tek farkı, 75°'lik açının 15° ve 60°'lik olarak farklı uzunluktaki açılara bölünmesidir(vi) (15 75 90 ) ÜÇGENİ b c = a h (Öklit alan bağıntısı) 4 3 = 5 AH AH = 5 12 br bulunur Cevap D'dir 16 m uzunluğundaki bir merdiven yer ile 45ISO GPStoleranssit 3 Geometriset toleranssit Kysymyspankki tekniikan alan oppilaitoksia varten 15 4 mm Geometriseen toleranssiin liittyvän mitan on aina oltava teoreettisesti tarkka TEDmitta ts laatikoitu mitta 75 Maksimimateriaalin vaatimusta Systems analysis and design alan dennis;

3 4 5 Ucgeni Ve Ozellikleri Not Bu
75 15 90 üçgeni alan
75 15 90 üçgeni alan- Şikayet üçgeninde şu bağıntılar vardır 1 (kök31)k (kök31)k (2kök2)k sırasıyla derecelerin karşılarındaki kenarların aralarındaki bağıntıdır bu 2 15 derecenin hemen yanına doğru bir doğru parçası indirerek ikizkenar üçgen oluşturup (1515 derece şeklinde) küçük bir 0 ve 15 75 90 üçgeni özelliği nedir?




30 60 90 Ucgeni
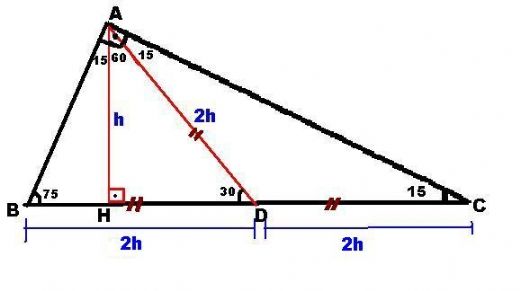
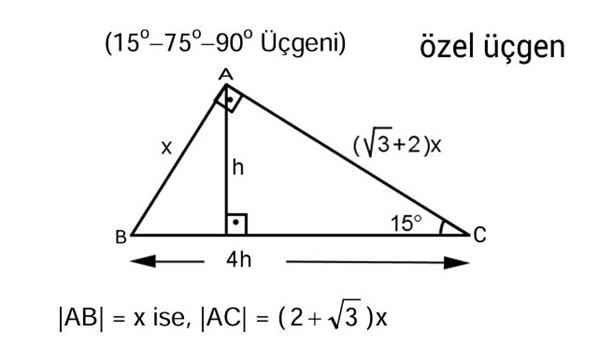
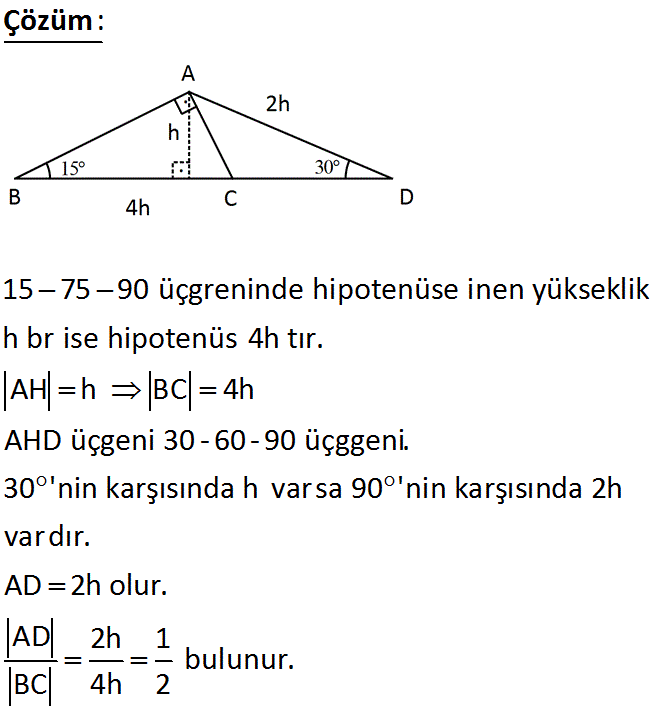
(A) açısı = 90 (B) açısı = 75 açısı = 15 açıları ise uzunlukları kurala şu şekilde olmak zorundadır (BC) = 30 cm (AB) = 25 cm (AC) = 5 cm olmak zorundadır 15 75 90 üçgeni özel kuralları yukarıda verildiği şekildedir Açılarını bilinmesiyle çok rahat uzunlukları da bilinmektedir Üçgeni (h4h) İSPAT onurcalis bu konuyu Geometri Formülleri forumunda açtı Cevap 2 Son mesaj 02 Eyl 14, 56 onurcalis bu konuyu Geometri Formülleri forumunda açtı Cevap 0 Son mesaj 02 Eyl 14, 1548Üçgeni Kenar Bağıntısı ( İSPAT ) ABC Üçgeninin Alanı = 1/24x4xsin30 olmak üzere 4x²dir ADC Üçgeninin alanı da bunun yarısı 2x²'dir
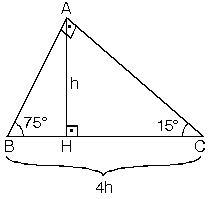
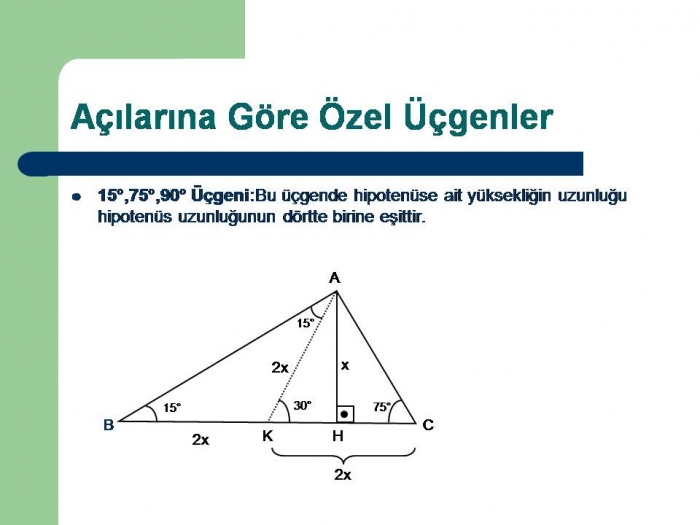
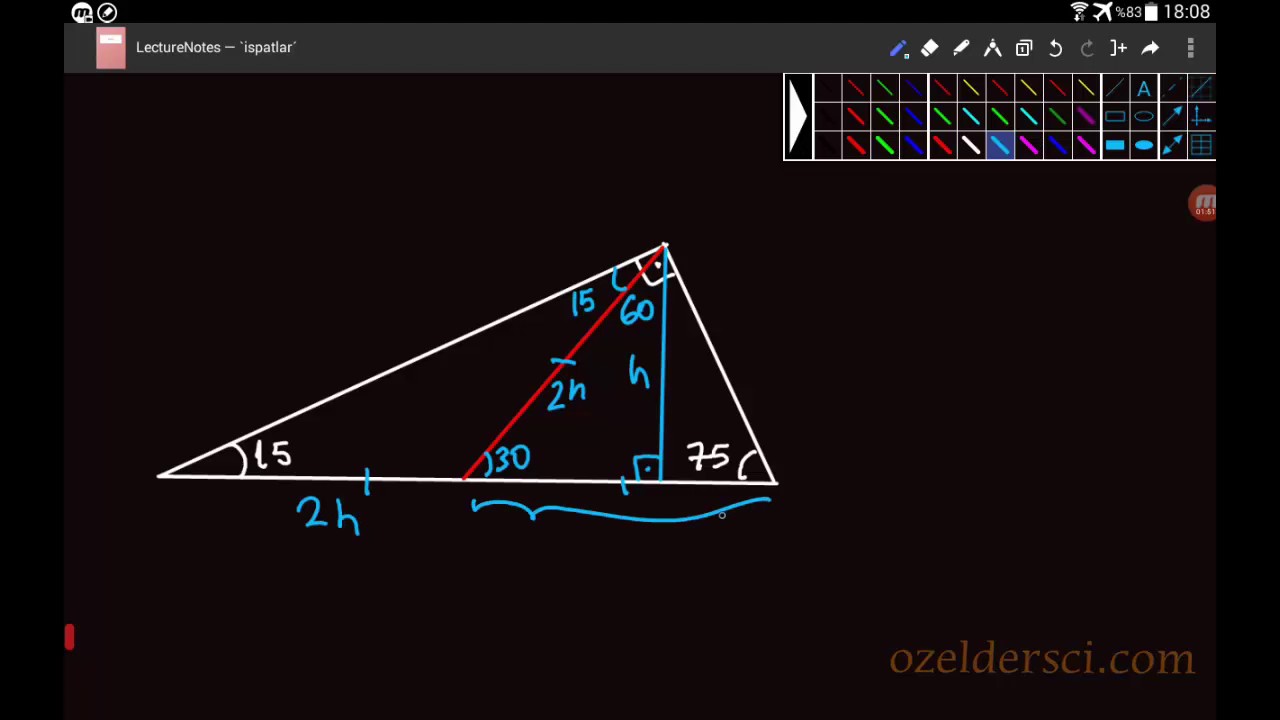
Bir üçgende iç açıları toplamı 180 derece olduğu için diğer açı 1 = 15 işleminden 15 derece olarak bulunur Yani bu üçgen 15 75 90 üçgenidir15 75 90 üçgeni alanı 16 Özel Üçgenler DİK ÜÇGEN Bir açısının ölçüsü 90° olan üçgene dik üçgen denir Dik üçgende 90° nin karşısındaki kenara hipotenüs, diğer kenarlara dik kenar adı verilir Hipotenüs üçgenin daima en uzun kenarıdırşekilde, m (A) = 90° BC kenarı hipotenüs AB ve AC kenarlarıdik kenarlardırİçKanalımıza abone olup videoları beğenerek bizi destekleyebilirsiniz
(15 75 90) Üçgeni konusunu önce anlatıyoruz hemen ardından etkileşime geçmesini sağlıyoruz Bu şekilde kalıcılığı ve öğrenmeyi sağlıyoruz Sizi ve arkadaşlarınızı sitemize bekliyoruz ) Tüm Öğrencilerimize İyi Dersler Diliyoruz ) Seyfettin KAHVECİA) 100 B) 110 C) 1 D) 130 E) 140 (19 ÖSS) ABC dik üçgeninde iç açılardan, m (BAC) = 30° m (CAD) = 90° – 30 「90 75 15 üçgeni alanı」の画像ギャラリー、詳細は各画像をクリックしてください。 Üçgeni (h4h) İSPAT;



1



15 75 90 Ucgeni Turleri Ve Ozellikleri
üçgeni bir ikizkenar dik üçgendir Üçgenin dik kenarları birbirine eşit ve hipotenüsü dik kenarların katıdır Oran aşağıdaki gibidir İspatı ise çok basittir Bir dik kenara 1 cm denilirse, ikizkenarlıktan dolayı diğer dik kenar da 1 cm olmak zorundadır Pisagor Teoremi 'nden deEn fazla kullanılan özel üçgenlerden birisi de 15 75 90 üçgeni olarak bilinmektedir Özel üçgenlerin bilinmesi özellikle de soru çözümleri sırasında büyük bir kolaylık sağlamaktadır 15 75 90 üçgenine göre muhteşem üçlü kuralının uygulanması da Açılar ve üçgenler 1 Açılar ve Üçgenler 70 soru ve cevap 1 Yandaki şekilde AB ⊥ AD, AC ⊥ BC, ABC açısının ölçüsü 60° olduğuna göre, EAD açısının ölçüsü aşağıdakilerden hangisidir?



Dik Ucgende Trigonometrik Hesaplamalar



Dik Ucgende Trigonometrik Oranlar Tyt Ayt 22 Yks 22 Uzaktan Egitim
45 45 90 üçgeni alan = a x a / 2 45 45 90 Üçgeninde Çevre NasılHaziran 1, 22 Haziran 8, 30 60 90 üçgeni kural Üçgene ait olan alan ve yükseklik biliniyorsa, Yani dik üçgende 30 derecenin karşısında yer alan kenar hipotenüsün yarısı 60 derecenin karşısında yer alan kenar 30 derecedir üçgeni;




Dik Ucgende Trigonometri Bikifi



2
(30° 60° 90°) dik üçgeninde; 15 75 90 Üçgeni Kuralı Nedir?Looking at the occurences of common prime factors in 75, 75, 15, and 90 we can see that the commonly occuring prime factors are 3 and 5 To calculate the prime factor, we multiply these numbers together GCF = 3 x 5 = 15 Find the GCF Using Euclid's Algorithm The final method for calculating the GCF of 75, 75, 15, and 90 is to use Euclid's




15 75 90 Ucgeni Ucgende Acilar Ve Ozel Ucgenler Ders Notlari Kunduz




Genler Gen Etler Ekenar Gen Kzkenar Gen Dk
Sinüs fonksiyonu karşı kenarın hipotenüse bölünmesidirBu videoda 15 75 90 üçgeninde hipotenüse ait yüksekliğin hipotenüsün dörtte birine eşit olduğunun sözsüz kanıtı yapılmıştır15 75 90 üçgeni, üçgeni,3Explore the full list of public IPv4 addresses by ranges from 0 to 254
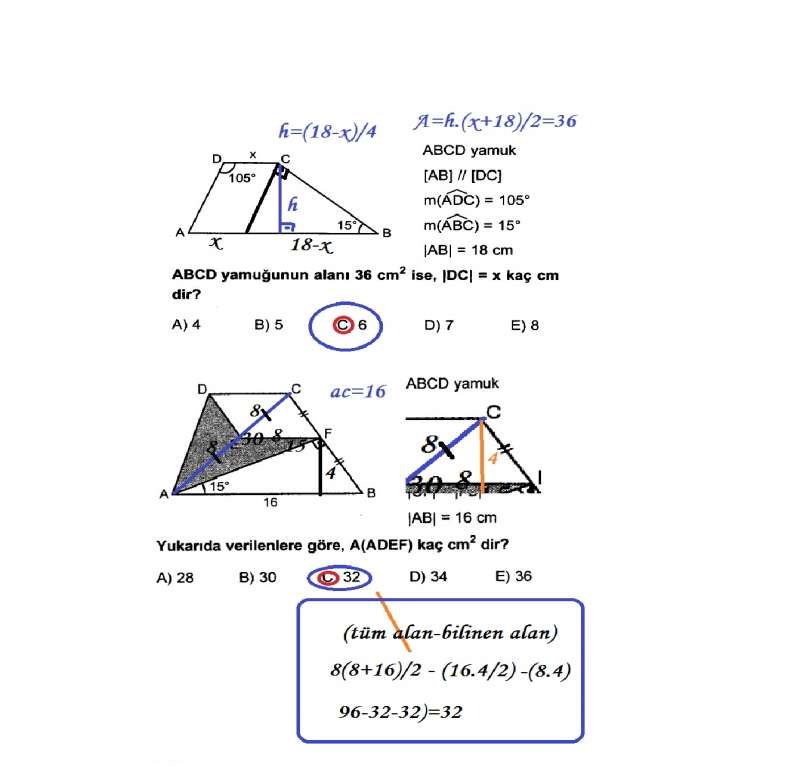



Yamuk
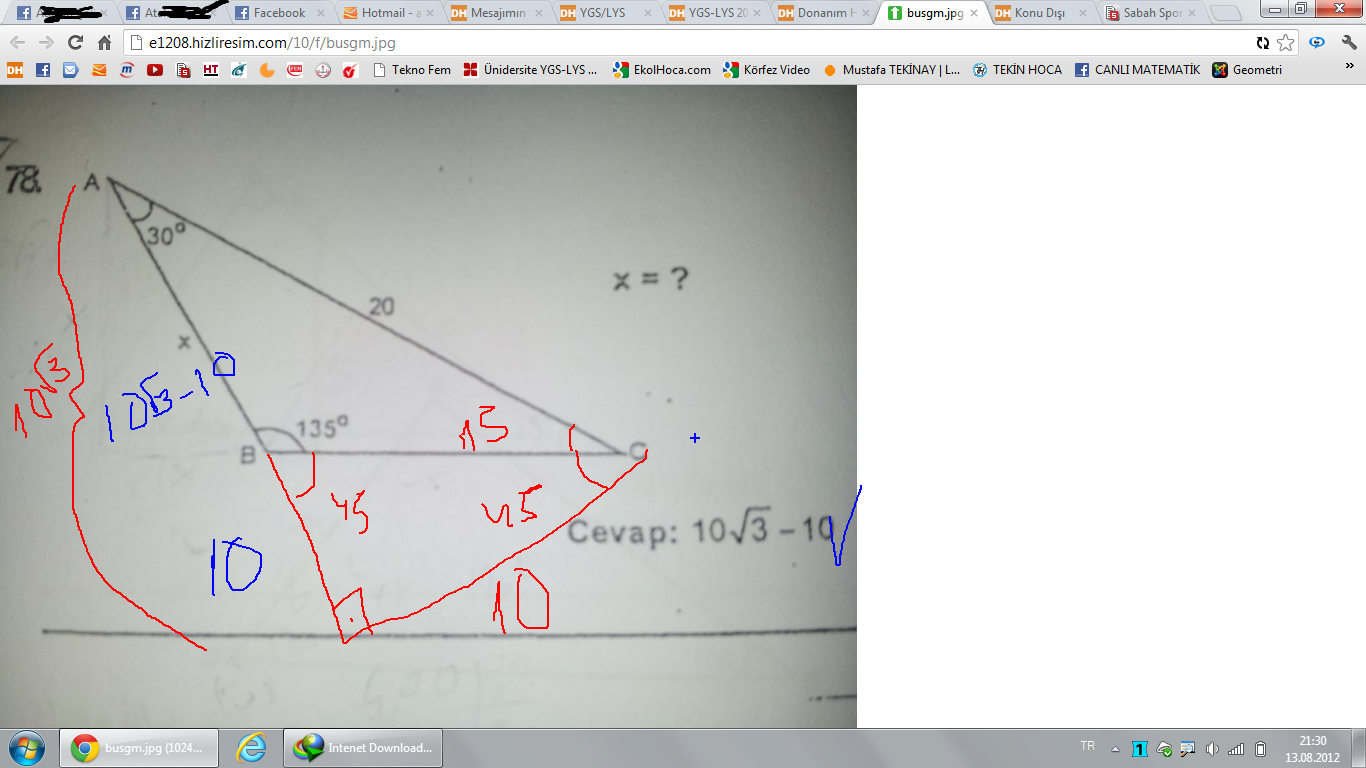



15 75 90 Ucgeni Donanimhaber Forum Sayfa 2
(15 75 90) Üçgeni (45 45 90) Üçgeni;Bu Youtube sayfasındaki sorularla ilgili daha ayrıntılı çalışmak için Android uygulamamızı aşağıdaki linkten indirebilirsinizUygulama içerisinde ipucu, çözü Örnek Bir 15 75 90 üçgeni düşünelim;
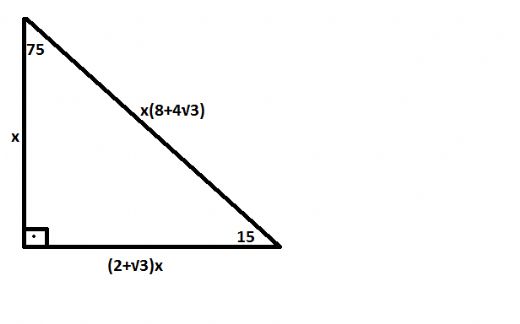



15 75 90 Ucgeninin Ozellikleri Nelerdir




22 5 67 5 90 Ucgeni Ozelligi Matematik Sarisin Renkli Okuma
About Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy & Safety How works Test new features Press Copyright Contact us Creators 15 75 90 ÜÇGENİ SORULARI 1 Bir ABC üçgeninde A açısı 90 derece B açısı 75 derecedir Bu üçgende hipotenüse ait yükseklik 3 cm dir Verilen bu bilgilere göre BC kenar uzunluğu kaç cm dir ?About Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy & Safety How works Test new features Press Copyright Contact us Creators
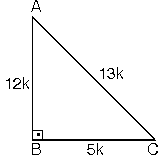



Dik Acili Ucgenin Kenar Ve Aci Ozellikleri Nedir



Rehber Aktarma
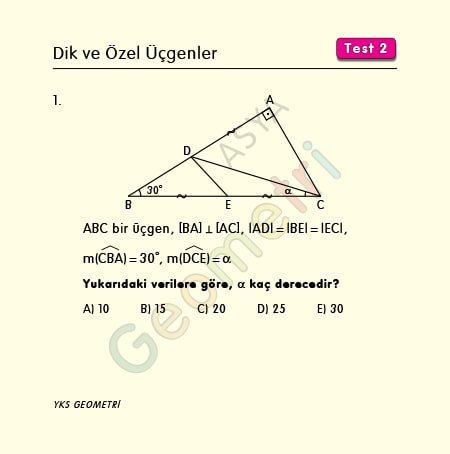
30°'lik açının karşısındaki kenar hipotenüsün yarısına eşittir 60°'lik açının karşısındaki kenar, 30° nin karşısındaki kenarın Ö3 katıdır 7 (30° 30° 1°) Üçgeni (30° 30° 1°) üçgeninde 30° lik açıların karşılarındaki kenarlara a Üçgen alanı hesaplama, önce bir kenar uzunluk ölçüsü alınır, bu kenar ölçüsüne ait yükseklik ölçüsü de alınır birbiriyle çarpılır, çıkan sonucu da ikiye böleriz, böylece üçgenin alanını hesaplamış oluruz Üçgenin alanını diğer bulma şekilleri ise;TYTAYT Geometri konuları dik ve özel üçgenler test2 ve çözümleri 30 60 90 üçgeni soruları, 45 45 90 üçgeni ile ilgili sorular, 15 75 90 üçgeni soruları, diklik merkezi soruları, muhteşem üçlü soruları, özel üçgen soru, pisagor bağıntısı soruları, 30 60 90 üçgeni çözümlü sorular, diklik merkezi soru çözümü, 15 75 90 üçgeni soru çözümü, pisagor
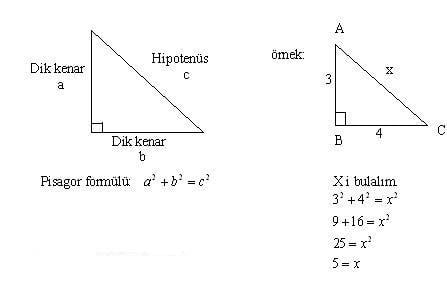



Dik Acili Ucgenin Kenar Ve Aci Ozellikleri Nedir



15 75 90 Ucgeni
üçgeni aynı zamanda bir dik üçgen olarak ifade edilmektedir Bu sebepten dolayı dik kesişen kenar uzunluklarından biri bilinirse kolayca alan bulunabilir Bu bağlamda 45 derecenin karşısındaki bir kenar, 'a' olursa o vakit alan formülü şu olur; Bu şekilde özellikleri ile beraber üçgeni üzerinden kolayca açı ve kenar uzunlukları bulunabilir Sadece bu değil aynı zamanda alan75 15 özel üçgeni 90 75 15 özel üçgeni 15 75 90 özel üçgeni kenar 15 75 90 özel üçgeni alan 15 75 özel üçgeni özellikleri 15 – 75 – 90 özel üçgeni 15 75 90 özel üçgeni özellikleri Yukarıda da dediÄŸimiz gibi bunları ezberlemek zorunda deÄŸilsiniz ancak bilirseniz size




22 5 67 5 90 Ucgeni Konu Anlatimi Ve Ozellikleri Eodev Com




30 60 90 Ucgeni
Üçgeni Kenar Bağıntısı ( İSPAT ) tenten1 bu konuyu Geometri Formülleri forumunda açtı Cevap 2 Son mesaj 02 Ağu 13, 33 üçgeni mrdanqerous bu konuyu Özel geometri soruları forumunda açtı Cevap 2Kenar ölçüsünden yararlanarak ve açısından yararlanarak iki şekildedir15 75 90 üçgeni



Dik Ve Ozel Ucgenler Test 2 Ders Geometri




3 4 5 Ucgeni Ve Ozellikleri Not Bu
üçgeninde şu bağıntılar vardır 1 (kök31)k (kök31)k (2kök2)k sırasıyla derecelerin karşılarındaki kenarların aralarındaki bağıntıdır bu 2 15 derecenin hemen yanına doğru bir doğru parçası indirerek ikizkenar üçgen oluşturup (1515 derece şeklinde) küçük bir 0 ve üçgeni 2 ayrı çözüm yöntemi bulunur bunlardan bir tanesi 75 derecelik açıyı 30 ve 45 olarak, diğeri de 15 ve 60 olarak bölmektir 30 ve 45 olarak böldüğünüzde karşınıza ya bir 30 60 90 üçgeni veya bir 45 45 90 üçgeni çıkacaktır 15 ve 60 olarak böldüğünüzde ise karşınıza bir 30 60 90 üçgeni ve de diğer tarafta kalan açıları 15 15 150 olan bir ikizkenar üçgenGeometri üzerindeki sabit açılar üzerinden ele alınan üçgenlerden biri üçgenidir Özellikle birçok farklı işlemi standart yapısı üzerinden kolayca yapma şansı tanır Kenarlar ile beraber alan ve çevre işlemleri bu açılır üzerinden çok daha kolay biçimde ele alınabilmektedir Üçgen




Dik Ucgen Konu Anlatimi Ve Ornek Soru Cozumu Kunduz




Math Off The Grid And Yet More 15 75 90 Fun
(15° 75° 90°) Üçgeni ile ilgili acil soru Idea question from @aylinaylin123 Geometri Novel Articles Register ;02Eyl17 Bu Pin, Mustafa YAZAGAN tarafından keşfedildi Kendi Pinlerinizi keşfedin ve 'e kaydedin! Geometride pek çok üçgen çeşidi bulunmaktadır Dik üçgenler bunlardan birisidir İç açılarından biri 90 derece olan üçgenlere dik üçgen adı verilmektedir Bu nedenle dik üçgenin diğer iki açısının toplamı da 90 derece olmalıdır Bunlar 1575




15 75 90 Ucgeni Webders Net



Dik Acili Ucgenin Kenar Ve Aci Ozellikleri Nedir
15 75 90 üçgeni özellikleri çoğu zaman dik bir üçgene dikme indirildiğinde ortaya çıkar Görselden de gördüğünüz gibi dik üçgenin, dik açısından tabana doğru bir dikme indirilmiş Daha sonra karşımıza iki adet 15 75 90 üçgeni çıkmış Yukarıdaki 15 75 90 üçgeni özellikleri, bu üçgenlerde kullanılarak sorunun doğru yanıtı bulunurLikes, 0 Comments Queen of Math (@geometrikmatematik) on Instagram "Özel üçgenlerden üçgeni #mathlovers #logaritma #ilovemath #matematik #math #geometri #geo"Search aylinaylin123 @aylinaylin123 October 1 27 Report (15° 75° 90°) Üçgeni ile ilgili acil soru MR1AY Verified answer 0 votes Thanks 0 More Questions From This User See All



15 75 90 Ucgeninin Ozellikleri Nelerdir



1




15 75 90 Ucgeni




15 75 90 Ucgeni Donanimhaber Forum




Ispat 15 75 90 Ucgeni Tyt Geometri Ozel Ucgenler Youtube




Ucgenlerde Uzunluk Matematik Ve Geometri




15 75 90 Ucgeni Ozellikleri Ve Kurallari




Dik Ucgen Derspresso Com Tr




Ucgenlerde Uzunluk Matematik Ve Geometri




30 60 90 Ucgeni Ve Ozellikleri Not Bu




30 60 90 Ucgeni Ozellikleri
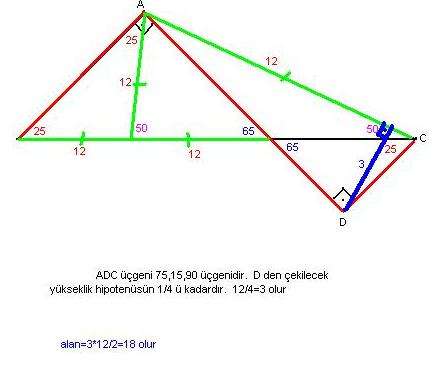



Ucgende Alan
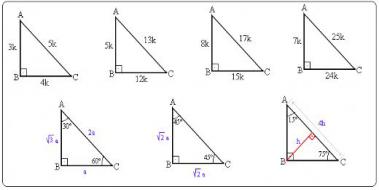



15 75 90 Ucgeninin Ozellikleri Nelerdir




Dik Ucgen 6 15 75 90 Ucgeni Geometri Metin Hocam Youtube
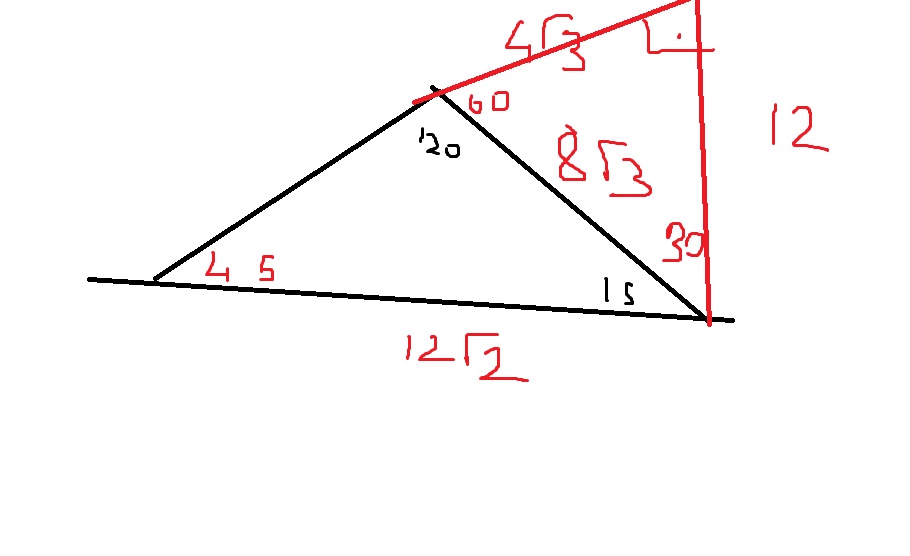



15 75 90 Ucgeni Donanimhaber Forum




4 Tane Ucgende Alan Sorulari
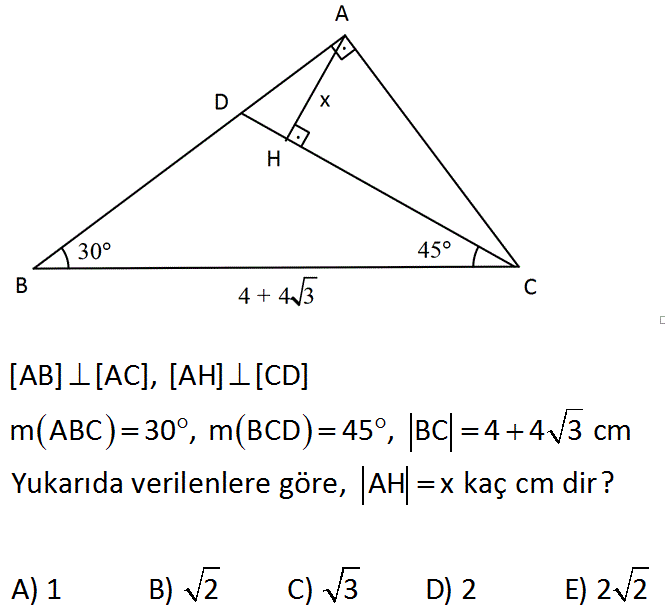



15 75 90 Ucgeni




Dik Ucgenler Pisagor Teoremi Konu Anlatimi Soru Cozumleri Ders Notu 9 Sinif Matematik Tyt
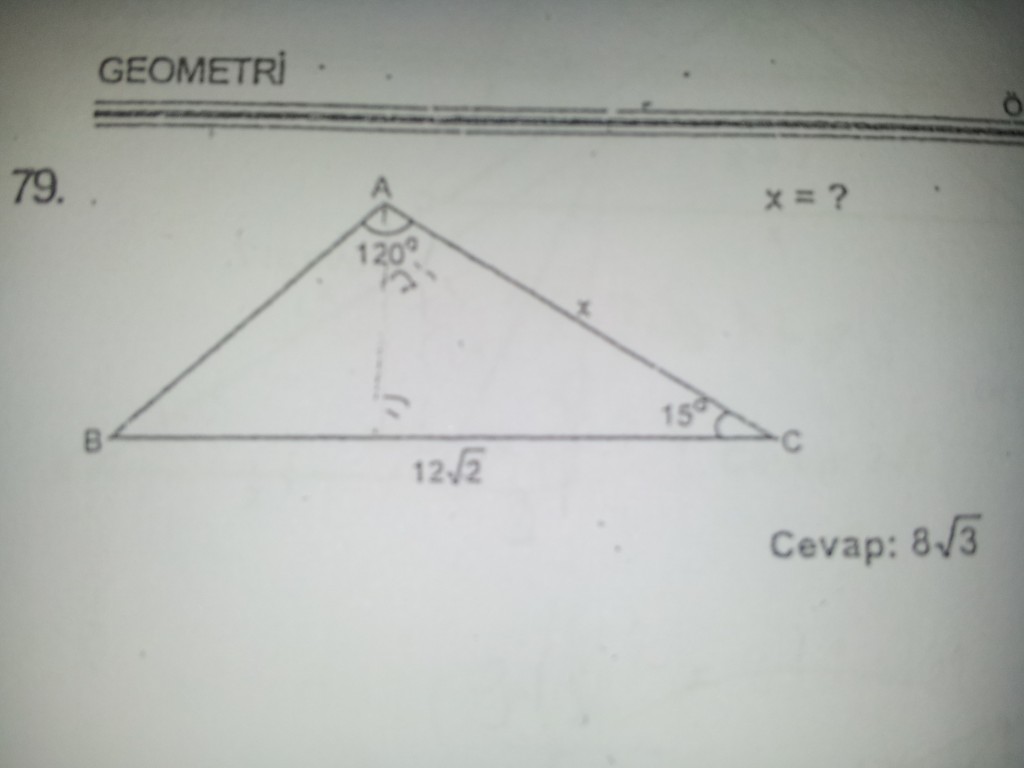



15 75 90 Ucgeni Donanimhaber Forum
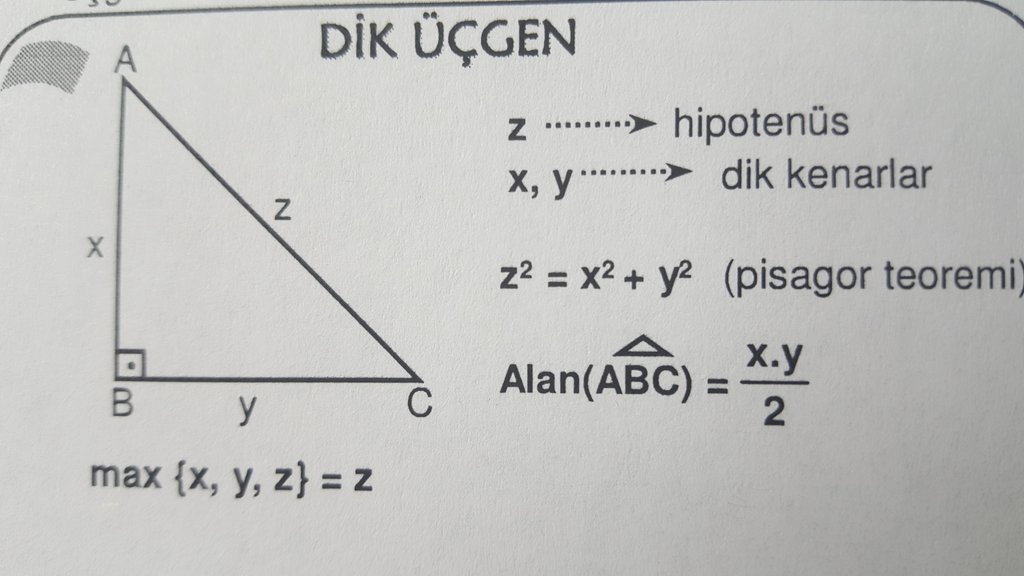



Mehmethoca46 Pratik Sosyalmedyamadokunma T Co Vo6wtpxgxe Twitter




15 75 90 Ucgeni Ispat Youtube




Net Fikir
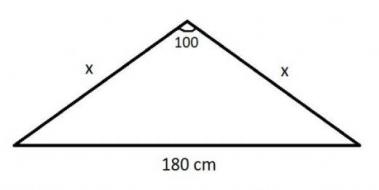



15 75 90 Ucgeninin Ozellikleri Nelerdir




Dik Ucgenler Pisagor Teoremi Konu Anlatimi Soru Cozumleri Ders Notu 9 Sinif Matematik Tyt




Dik Ucgen Oklid Bagintisi 30 60 90 Ucgeni Kurali




Ikizkenar Ucgen Alani Nasil Bulunur Ikizkenar Ucgenin Alanini Hesaplama Formulu Nedir Son Dakika Egitim Haberleri
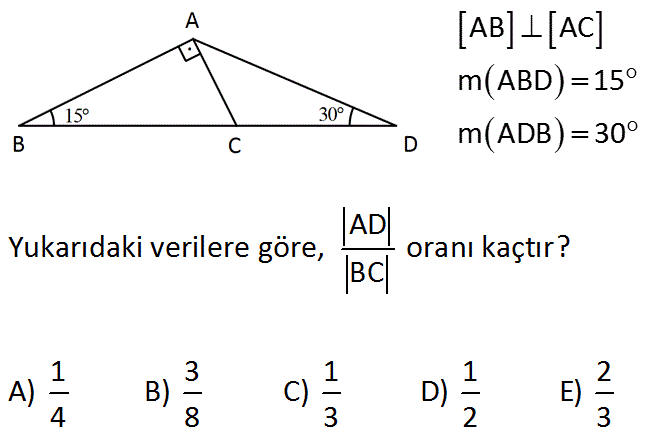



15 75 90 Ucgeni




Net Fikir
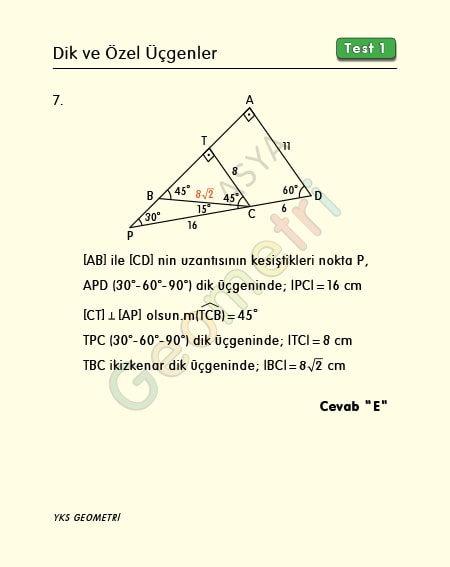



Dik Ve Ozel Ucgenler Test 1 Ders Geometri




Dik Ucgen Oklid Bagintisi 30 60 90 Ucgeni Kurali




Ucgende Alan Formulleri Ve Bagintilari Matematik Ogretmenleri



15 75 90 Ucgnler Sitem




Ozel Ucgenler Pdf




Net Fikir




Dik Ucgen Oklid Bagintisi 30 60 90 Ucgeni Kurali



15 75 90 Ucgeni Kurali Nedir 15 75 90 Ucgeninin Ozellikleri Nelerdir Egitim Haberleri



45 45 90 Ucgeni Matematikce




15 75 90 Ucgeni Ucgende Acilar Ve Ozel Ucgenler Ders Notlari Kunduz




Acilarina Gore Ucgenler Ppt Indir
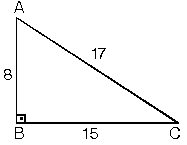



Dik Ucgen Ve Ozellikleri




15 75 90 Ucgeni Ucgende Acilar Ve Ozel Ucgenler Ders Notlari Kunduz




15 75 90 Ucgeni Kurali Nedir 15 75 90 Ucgeni Alan Ve Kenar Bagintilari Konu Anlatimi
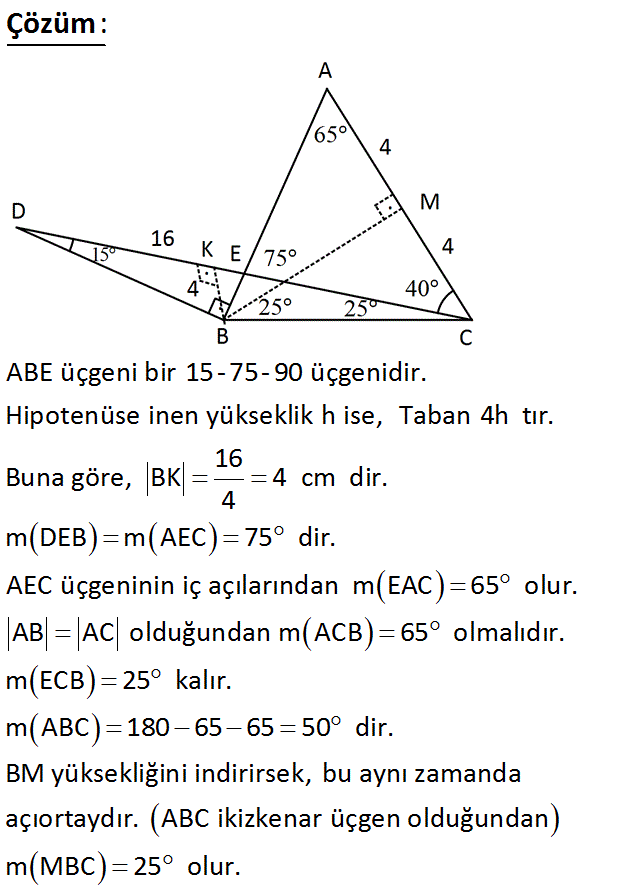



15 75 90 Ucgeni




15 75 90 Ucgeni
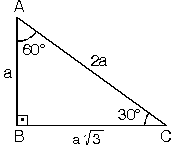



8 15 17 Ozel Ucgeninin Ic Acilari Nedir




Calameo Tyt Geometri 8 Ogrencilik Multi Kutu Test




15 75 90 Ucgeni Ucgende Acilar Ve Ozel Ucgenler Ders Notlari Kunduz
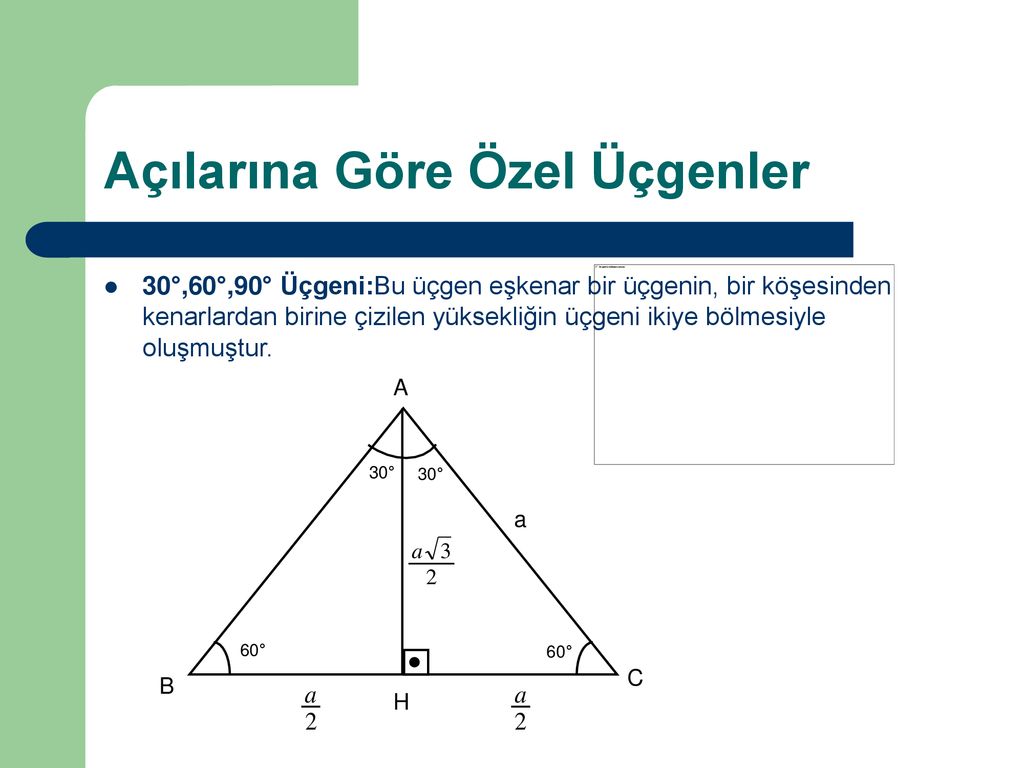



30 60 90 Ucgeni




Dik Ucgen 17 22 5 67 5 90 Ucgeni Ders Calisma Ipuclari Evde Egitim Matematik




Dik Ucgenler Pisagor Teoremi Konu Anlatimi Soru Cozumleri Ders Notu 9 Sinif Matematik Tyt




15 75 90 Ucgeni Not Bu




30 60 90 Ucgeni Ozellikleri




15 75 90 Ucgeni
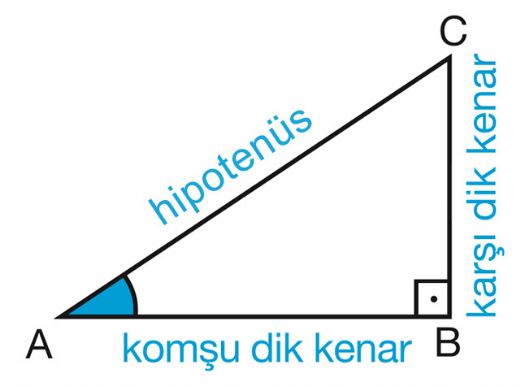



Dik Ucgen Ve Trigonometri
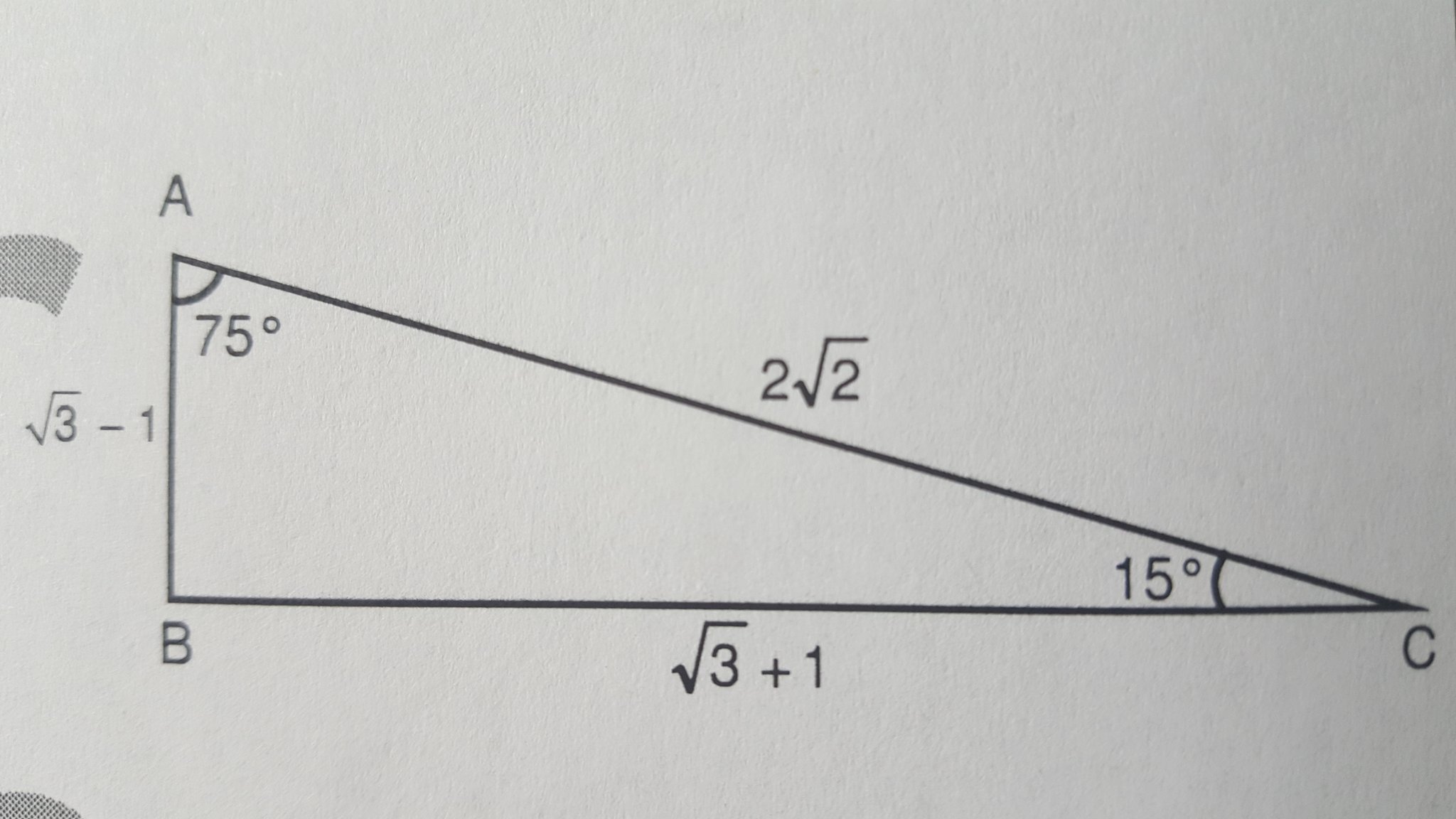



Mehmethoca46 Pratik Sosyalmedyamadokunma T Co Vo6wtpxgxe Twitter




15 75 90 Ucgeni Not Bu




Calameo Ayt Geometri 8 Ogrencilik Multi Kutu Test
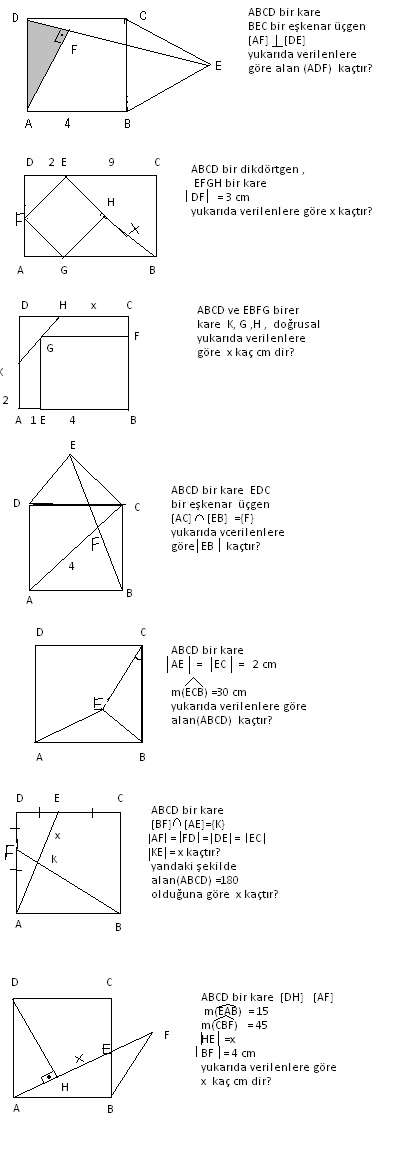



Kare Sorulari Lutfen Yardimci Olurmusunuz Acillll




Geometrik Kavramlar Geometride Nokta Dogru Duzlem Gibi Kavramlar Tanimsiz Olarak Kabul Edilir Ppt Indir



Top 19 23 67 90 Ucgeni En Iyi 22




Net Fikir




Dik Ucgen 16 15 75 90 Ucgeni Matematik Felsefesi Temel Matematik Evde Egitim
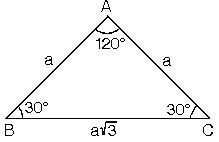



Dik Acili Ucgenin Kenar Ve Aci Ozellikleri Nedir




Dik Ucgen Konu Anlatimi Ve Ornek Soru Cozumu Kunduz




Dik Ucgen Oklid Bagintisi 30 60 90 Ucgeni Kurali




15 75 90 Ucgeni Ucgende Acilar Ve Ozel Ucgenler Ders Notlari Kunduz




15 75 90 Ucgen Ozelligi Ve 5 Ornek Cozum Youtube




Net Fikir



Kare Alan Matematik Kafasi




Dik Ucgen Oklid Bagintisi 30 60 90 Ucgeni Kurali



15 75 90 Ucgeni Ozelliklerinin Ispati Youtube




30 60 90 Ucgeni Kurali Nedir Ve Ozellikleri Nelerdir 30 60 90 Dik Ucgeni Ispati Ve Ornekleri Konu Anlatimi



1



45 45 90 Ucgeni Kurali Nedir 45 45 90 Ucgeninin Ozellikleri Nelerdir En Son Haberler




Dik Ucgenin Alani Nasil Bulunur Dik Ucgenin Alani Nasil Hesaplanir Formulu Nedir Egitim Haberleri




Math Off The Grid And Yet More 15 75 90 Fun


