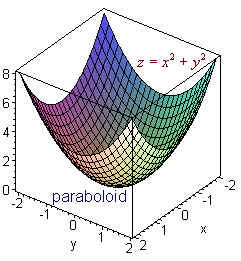
3dprinting, solidworks f(0,0,0) is 0, not 1 (the isosurface level), so you only get points drawn completing the cones if there are enough points near the origin that happen to have value 1 But when you switch to linspace(,,), the closest coordinates to the origin are at about 105, leaving a gap of about 21Tại `(x;y;z)=(0;1;1)` `x^2y^2z^2 = xy3y2z3` TínhZ = x2 y2 and the plane z = 4, with outward orientation (a) Find the surface area of S Note that the surface S consists of a portion of the paraboloid z = x2 y2 and a portion of the plane z = 4 Solution Let S1 be the part of the paraboloid z = x2 y2 that lies below the plane z = 4, and let S2 be the disk x2 y2 ≤ 4, z = 4 Then

How To Plot Z 5 Sqrt X 2 Y 2 0 Le Z Le 5 In Mathematica Mathematics Stack Exchange
F(x+y+z x^2+y^2+z^2)=0
F(x+y+z x^2+y^2+z^2)=0-We see by inspection therefore that (8) n = xi yj zk a, where we have divided by a to make n a unit vectorWolframAlpha brings expertlevel knowledge and capabilities to the broadest possible range of people—spanning all professions and education levels




Vector Analysis By Alimkanwalimtinaa Issuu
Examples of Subspaces Example 1 The set W of vectors of the form (x, 0) where x ∈ R is a subspace of R2 because W is a subset of R2 whose vectors are of the form (x, y) where x ∈ R and y ∈ R The zero vector (0, 0) is in W (x1, 0) (x2, 0) = (x1 x2, 0) , closure under addition r ⋅ (x, 0) = (rx, 0) , closure under scalarFactor x^2y^2 x2 − y2 x 2 y 2 Since both terms are perfect squares, factor using the difference of squares formula, a2 −b2 = (ab)(a−b) a 2 b 2 = ( a b) ( aReduza a equação $x^2y^27z^216xy8xz8yz$ de forma a identificar a quádrica que ela representa e esboce o seu gráfico 1217 Reduza a equação $4x^23y^2z^212xy4xz8yz$ de forma a identificar a quádrica que ela representa e esboce o seu gráfico 1224
A sphere is the graph of an equation of the form x 2 y 2 z 2 = p 2 for some real number p The radius of the sphere is p (see the figure below) Ellipsoids are the graphs of equations of the form ax 2 by 2 cz 2 = p 2, where a, b, and c are all positiveEg x2p y2q = z is a linear in z and of first order Further, a pde is said to be quasilinear if degree of highest order derivative is one, no product of partial derivatives are present eg z – z xx (z y)2 = 0 is a quasilinear 2nd order 112 FORMATION OF PARTIAL DIFFERENTIAL EQUATIONSSphere x2 y2 z2 = a2 lying in the first octant (x,y,z,≥ 0) Solution Once again, we begin by finding n and dS for the sphere We take the outside of the sphere as the positive side, so n points radially outward from the origin;
Điều sau có đúng hay không?This video explains how to convert a rectangular equation (cone) to a spherical equationhttp//mathispower4ucomThe temperature at a point (x,y,z) on the surface of a metal is T(x,y,z) = 0e −x2 3y2−9z2 where T is measured in degree Celsius and x, y, z in meters (a) In which direction does the temperature increase fastest at the point P(2,−1,2)?



Surfaces




Surfaces Part 2
0 2 4 6 8 10 x 0 2 4 6 8 10 y 0 25 5 75 10 z f(x,y)=y Notare che il piano passa per l'asse x e interseca il piano yz sulla retta y = z 0 25 5 75 10 x 0 25 5 75 y 10 0 5 10 15 z f(x,y)=x y Notare che il piano passa per l' origine e interseca il piano yz sulla retta yNot a problem Unlock StepbyStep 设x^2y^2z^24z=0,求x的2阶偏导 15 已知函数z=z(x,y)由方程x^2y^2z^2=e^z 4 设函数z=f(x,y)由方程x2y2z22z6=0,



What Is The Graph Of X 2 Y 2 Z 2 1 Quora
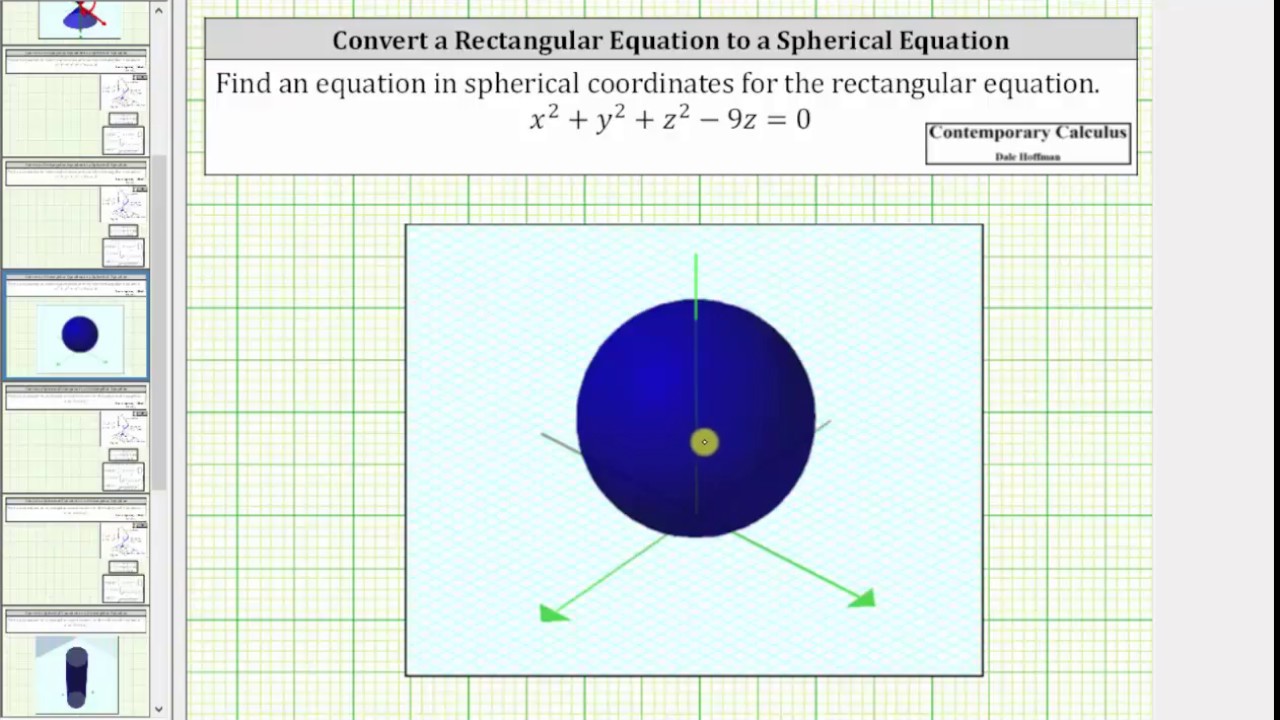



Convert A Rectangular Equation To A Spherical Equation X 2 Y 2 Z 2 9z 0 Youtube
Y = 1 Parabola z = x2 1 y = 2 Parabola z = x2 4 y = 3 Parabola z = x2 9 (d) Sketch all the traces that you found in part (c) on the same coordinate axes 5 (e) Below is the graph of z = x2 y2 On the graph of the surface, sketch the traces that you found in parts (a) and (c)Take the square root of both sides of the equation x^ {2}y^ {2}z^ {2}=0 Subtract z^ {2} from both sides y^ {2}x^ {2}z^ {2}=0 Quadratic equations like this one, with an x^ {2} term but no x term, can still be solved using the quadratic formula, \frac {b±\sqrt {b^ {2}4ac}} {2a}, once they are put in standard form ax^ {2}bxc=0Where S is the hemisphere given by x2 y2 z2 = 1 with z ≥ 0 Solution We first find ∂z ∂x etc These terms arise because dS = q 1(∂z ∂x) 2 (∂y) 2dxdy Since this change of variables relates to the surface S we find these derivatives by differentiating both sides of the surface x2 y2 z2 = 1 with respect to x, giving 2x2z∂



If X 2 Y 2 Z 2 2xyz 1 Then Prove That Dx 1 X 2 Dy 1 Y 2 Dz 1 Z 2 0 Sarthaks Econnect Largest Online Education Community



1
It shows the paraboloid z = A x 2 B y 2 over the square domain1 ≤ x ≤ 11 ≤ y ≤ 1 If you change the domain to a disk, you will see the portion of the paraboloid for which 0 ≤ z ≤ 8 When you change A and B, the domain will change accordingly Here are a few things to think aboutWe can plot with this transform Remember that the dependent variable is the height, and the independent variables are the radius and the azimuth (in that order) sage plot3d(9r^2, (r, 0, 3), (theta, 0, pi), transformation=T) Graphics3d Object We next graph the function where the radius isSpherical coordinates to rewrite the triple integral as an iterated integral The sphere x2 y2 z2 = 4 is the same as ˆ= 2 The cone z = p 3(x2 y2) can be written as ˚= ˇ 6 (2) So, the volume is Z 2ˇ 0 Z ˇ=6 0 Z 2 0 1 ˆ2 sin˚dˆd˚d 5 Write an iterated integral which gives the volume of the solid enclosed by z2 = x2 y2, z= 1




Find The Shortest And Longest Distances From The Point P 5 2 3 To The Surface Of The Sphere X 2 Y 2 Z 2 2 X 2z 2 Homeworklib




Se11g01 02 Gif
X2 y2 (z − 1)2 = 1 I ρ = 2 is a sphere radius 2 and φ ∈ 0,π/2 says we only consider the upper half of the sphere 2 2 y z 1 2 rho = 2 x rho = 2 cos ( 0 ) Triple integral in spherical coordinates (Sect 157) Example Use spherical coordinates to find the volume of the region outside请输入验证码以便正常访问 由360提供技术支持 网络或服务器异常 向右滑动滑块填充拼图 您的IP是:2186 如果经常出现此页面,请把您的IP和反馈意见 提交 给我们,我们会尽快处理,非常感谢。 为什么会出现验证码? 出现验证码表示您所在的网络 回答量: 811 采纳率: 68% 帮助的人: 179万 我也去答题 访问个人页 关注 展开全部 z^2=x^2y^2的图像如下图所示: 通过一个定点V且与定曲线r (它不过定点V)相交的所有直线构成的曲面称为锥面;如果母线是和旋转轴斜交的直线,那么形成的旋转面叫做圆锥面




Homework Assignment 4 Math 253



The Point Of Intersection Of The Line Passing Through 0 0 1 And Intersecting The Lines X 2y Z 1 X Y 2z 2 And X Y 2 X Z 2 With Xy Plane Is A Left Frac 5 3 Frac 1 3 0 Right B 1 1 0 C Left Frac 2 3
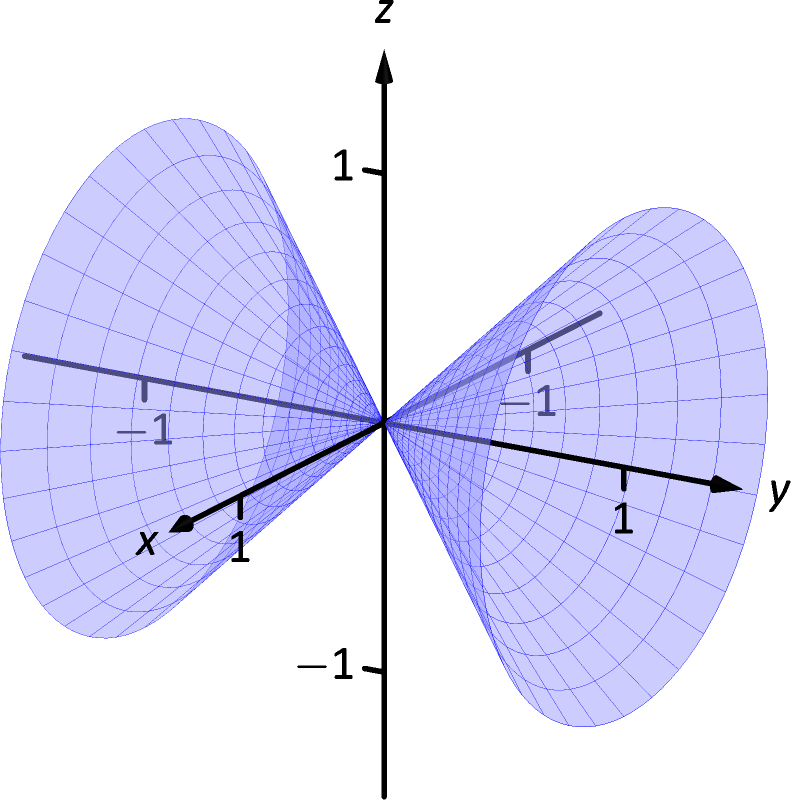
12 EpsilonDelta Definition of a Limit This section introduces the formal definition of a limit Many refer to this as "the epsilondelta,'' definition, referring to the letters ϵ and δ of the Greek alphabet Before we give the actual definition, let's consider a few informal ways of describing a limit Given a function y = f(x) and an xMinimize the function f(x, y, z)=x^{2}y^{2}z^{2} subject to the constraints x2 y3 z=6 and x3 y9 z=9 Get certified as an expert in up to 15 unique STEM subjects this summer Our Bootcamp courses are free of charge3 Answers3 Write it as x 2 z 2 = y 2 Note that y is the hypotenuse of a triangle with length x and height z So, this forms a circular cone opening as you increase in y or decrease in y This figure is the (double) cone of equation x 2 = y 2 − z 2 The gray plane is the plane ( x, y) You can see that it is a cone noting that for any y




Oneclass If X2 Y2 Lt Z Lt 1 Find The Maximum And Minimum Of The Function U X Y Z X Y Z
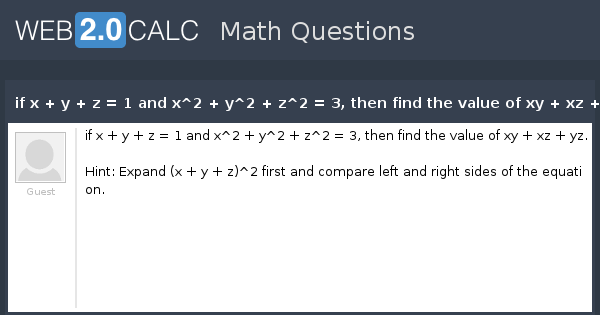



View Question If X Y Z 1 And X 2 Y 2 Z 2 3 Then Find The Value Of Xy Xz Yz
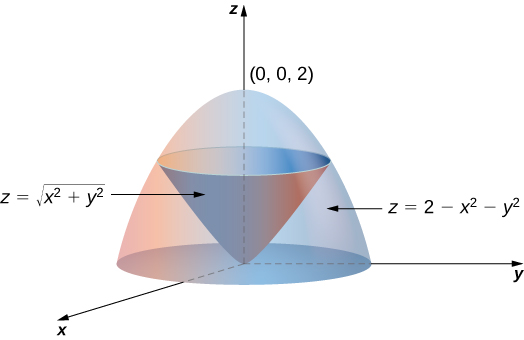
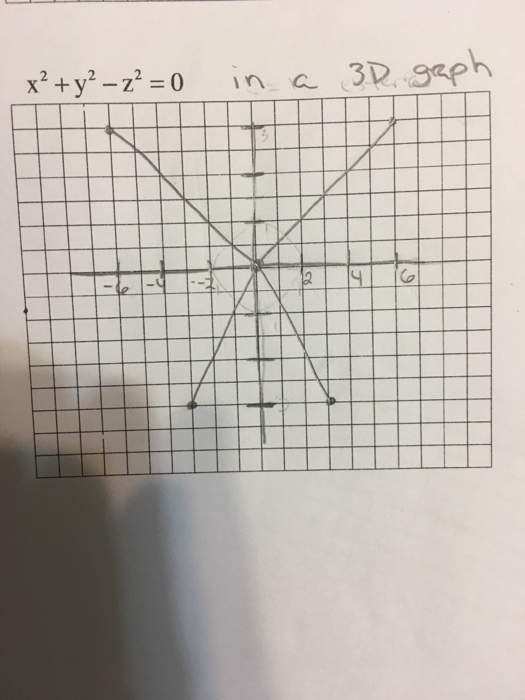
Example 1586 Setting up a Triple Integral in Spherical Coordinates Set up an integral for the volume of the region bounded by the cone z = √3(x2 y2) and the hemisphere z = √4 − x2 − y2 (see the figure below) Figure 15 A region bounded below by a cone and above by a hemisphere Solution F p × acts on the set of solution by coordinatewise multiplication, where we have ( c x, c y, c z) = ( x, y, z) iff c = 1 or x = y = z = 0, that is all orbits except that of the trivial solution have length p − 1 We conclude that p − 1 ∣ m − 1, hence together with p ∣ m m ≡ p ( mod p 2 − p) by the Chinese Remainder TheoremSee the answer Show transcribed image text Expert Answer Previous question Next question Transcribed Image Text from this Question x^2 y^2 z^2 = 0 in a 3D graph Get more help from Chegg Solve it with our calculus problem solver and calculator




Lagrange Multipliers Ppt Download
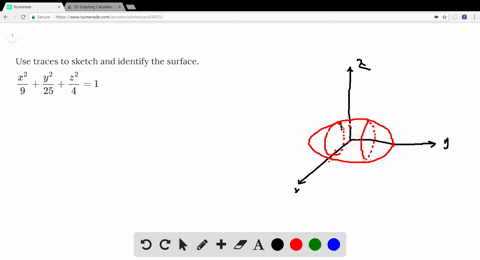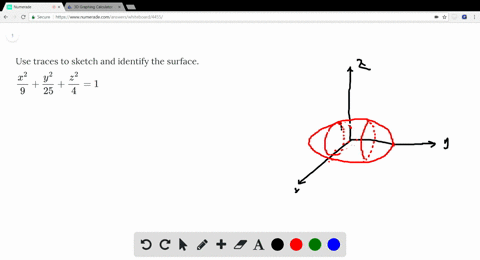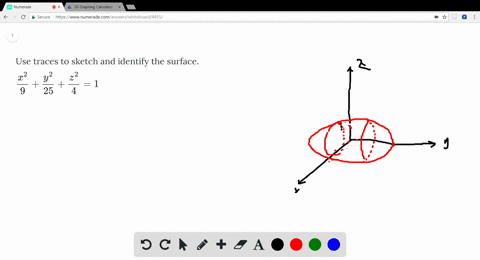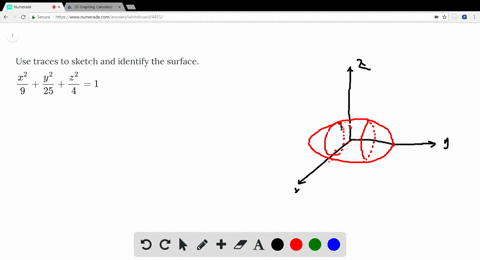



Solved Use Traces To Sketch And Identify The Surf
X^2y^2z^2=1 WolframAlpha Rocket science?Se trata de calcular el volumen interior a la esfera x2 y2 z2 = R2 y exterior al paraboloide circular x 2 y 2 =4a(za), con R>a>0 (Figura6c) Las ecuaciones de estas superficies en coordenadas cilíndricas son, respectivamente, r 2 z 2 = R 2 y r 2 =The quadratic formula gives two solutions, one when ± is addition and one when it is subtraction x^ {2}2yxy^ {2}=0 x 2 2 y x y 2 = 0 This equation is in standard form ax^ {2}bxc=0 Substitute 1 for a, 2y for b, and y^ {2} for c in the quadratic formula,



If X 2 Y 2 Z 2 2 X Y Z 3 What Is The Value Of 2x 3y 4z Quora




John Lesieutre Multiplicities
X (2 − 2x)2 2 dx = √ 6 Z 1 0 (2x3 − 4x2 2x)dx = √ 6 h1 2 x4 − 4 3 x3 x2 i 1 0 = √ 6 6 (b) ZZ S zdS, where S is the part of the paraboloid z = x2 y2 under the plane z = 4 Solution With Q = {(x,y) x2 y2 ≤ 4} = {(r,θ) 0 ≤ r ≤ 2,0 ≤ θ ≤ 2π}, we have ZZ S zdS = ZZ Q (x2 y2) s ∂z ∂x 2Trigonometría Gráfico x^2y^22x=0 x2 − y2 − 2x = 0 x 2 y 2 2 x = 0 Halle la forma estándar de la hipérbola Toca para ver más pasos Complete el cuadrado para x 2 − 2 x x 2 2 x Toca para ver más pasos Usa la forma a x 2 b x c a x 2 b x c para encontrar los valores de a a, b b y c c a = 1, b = − 2, c = 0 aIt's the equation of sphere The general equation of sphere looks like math(xx_0)^2(yy_0)^2(zz_0)^2=a^2/math Wheremath (x_0,y_0,z_0)/math is the centre of the circle and matha /math is the radious of the circle It's graph looks



Www Ualberta Ca Csproat Homework Math 215 Solution 7 Pdf




Solve The System Of Equations 3x 3y 2z 1 X 2y 4 10y 3z 2 And 2x 3y Z 5 Answer Mathematics 1 Question Answer Collection
Question X^2 Y^2 Z^2 = 0 In A 3D Graph This problem has been solved!X2 y2 z2 = 0 Math 9 Assignment 1 Solutions 3 7 The partial di erential equation @2u @x2 @2u @y2 = 0 is called Laplace's Equation, named after the eminent French mathematician Pierre Simon de Laplace (1749 17) Solutions of this equation are called harmonic functions and play a role in problemsを用いても,直ちに示せる. =r より x 2 y 2 =r 2 ※ 点 P が座標軸上(通俗的に言えば,赤道上または北極,南極の場所)にあるとき,直角三角形にならないが,たとえば x 軸上の点 (r , 0) についても, r 2 0 2 =r 2 が成り立つ.このように,座標軸上の点については直角三角形はできないが,この




If X2 Y2 Z2 2 X Y Z 3 Find The Value Of 2x 3y 4z Brainly In



Search Q X 5e2 2by 5e2 2bz 5e2 3d9 Tbm Isch
例 z ≡ 0 (x,y によらずにz は常に0) はz = x2 y2 が定め る曲面の原点(0,0,0) における接平面である。(この場合一次 の係数A = B = 0) 実際、点(x,y) と原点との距離は p x2 y2 なので (x,y) → (0,0) 即ち p x2 y2 → 0 のとき x2 y2 p x2 y2 → 0 練習問題 は が定める曲面の原点The points (x,y,z) of the sphere x 2 y 2 z 2 = 1, satisfying the condition x = 05, are a circle y 2 z 2 = 075 of radius on the plane x = 05 The inequality y ≤ 075 holds on an arc The length of the arc is 5/6 of the length of the circle, which is why the conditional probability is equal to 5/6X 2 、y 2 、z 2 =0,0,1 ないしその入れ替えである。 よって x、y、zの何れか2個は偶数であり、互いに素にはならない。 (A) x,y,zの最大公約数が1とすれば この問題はクリアできるが、解が多数になる。




If X X 1 X 2 Represents




How To Plot X 2 Y 2 Z 2 Mathematics Stack Exchange
4 Integrali tripli esercizi svolti Osserviamo che › µe l'insieme dei punti compresi fra il semicono di equazione z = 2 p x2 y2 e il piano di equazione z = x 2 Integrando per flli paralleli all'asse z, si ha che Z › 2zdxdydz = 2 Z D "Z x2 2 p x2y2 zdzX 2 y = lim x!0 0 x2 = 0 6= 3 The function is continuous on the set f(x;y) 2R2j(x;y) 6= (0 ;0)g Created Date 7/3/14 PMX 2 y2) j cos j = jzj p 2 p x 2 y2 = 1 p 2 La curva intersecci on de la super cie esfe rica y la super cie co n ica es (x 2 y2 = z2 x 2 y2 z2 = 2 by x y z B b El cilindro que proyecta sobre el plano XY se obtiene eliminando z en esas ecuaciones 2x 22 y = 2 by , x y2 = by , x 2 y b 2 2 = b2 4 Por tanto, la proyecci on de sobre




Plot Of A Portion Of The Variety X 2 Y 2 Z 2 Z 3 0 Download Scientific Diagram




Elliptic Paraboloid X 2 Y 2 Z 2 0 Download Scientific Diagram
WolframAlpha brings expertlevel knowledge and capabilities to the broadest possible range of people—spanning all professions and education levels How to find the center, radius, and equation of the sphere The formula for the equation of a sphere We can calculate the equation of a sphere using the formula ( x − h) 2 ( y − k) 2 ( z − l) 2 = r 2 (xh)^2 (yk)^2 (zl)^2=r^2 ( x − h) 2 ( y − k) 2 ( z − l) 2 = r 2 where ( h, k, l) (h,k,l) ( h, k, l) is the center of 3Dplot of "x^2y^2z^2=1" Learn more about isosurface;



Surface Integrals




Assignment 5 Math 215 Q1 1 Evaluate The Triple Integral A



Triple Integrals In Cylindrical And Spherical Coordinates Calculus Volume 3




How Do You Solve 2x 9y 2 X 2y 3z 0 And Y Z 1 Using Matrices Socratic




Proof Of Lemma 3 2 The Plane Ax By Cz 0 Intersects The Cone X 2 Download Scientific Diagram
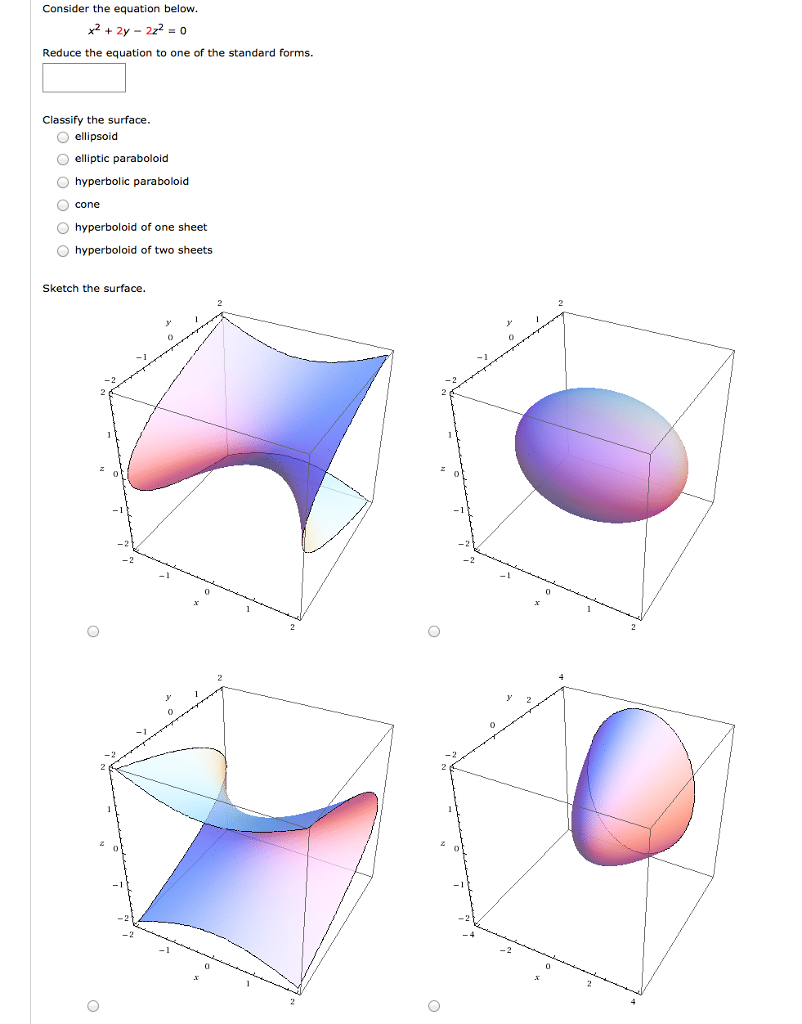



Consider The Equation Below X 2 2y 2z 2 0 Chegg Com




Algebra Precalculus



How To Find X In Terms Of Y And X In The Equation X 2 Xy Z 2 0 Quora




A Quadratic Surface Is Sketched Determine Which Of The Given Equations Best Fits The Graph Show Traces Y 2 Z 1 And X 0 For Each One A
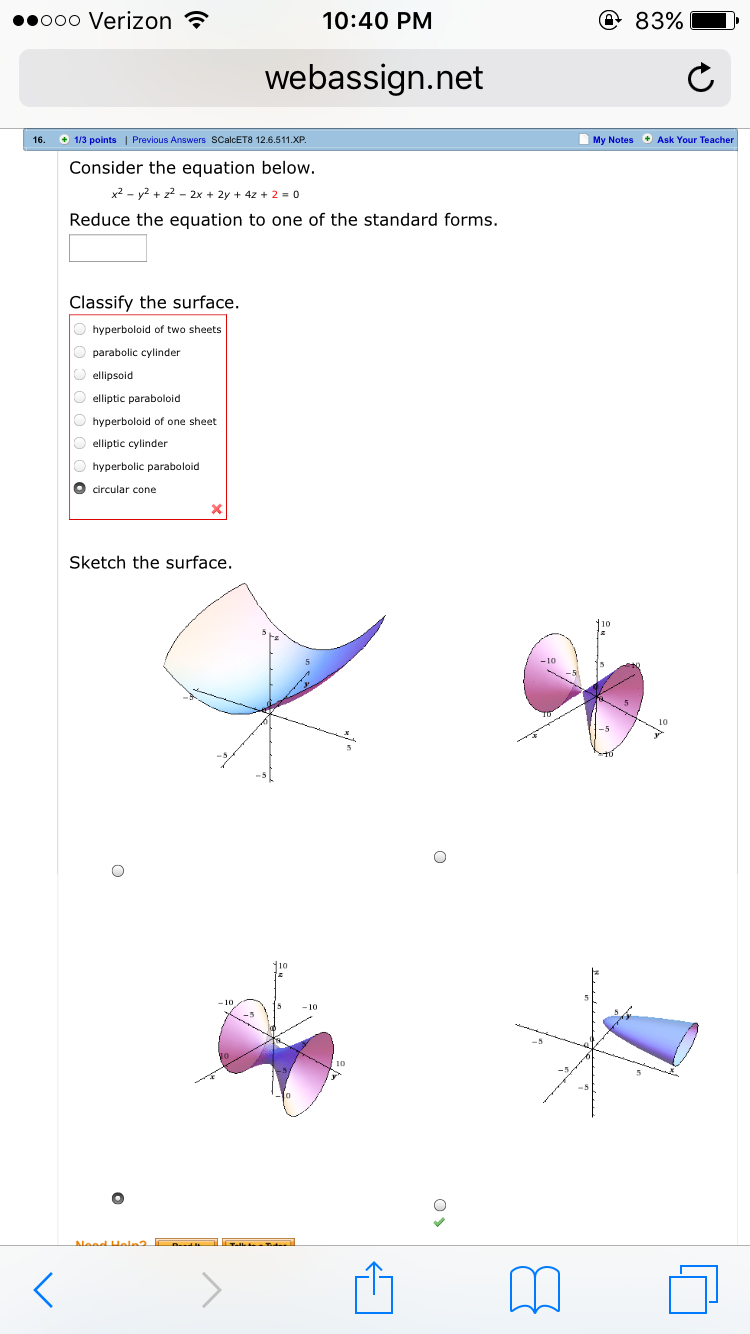



Consider The Equation Below X 2 Y 2 Z 2 2x Chegg Com



Http Www Math Drexel Edu Faculty Dmitryk Wp Content Uploads Sites 6 14 01 Exam2 Solutions Pdf



Http Www Math Drexel Edu Classes Calculus Resources Math0hw Homework11 7 Ans Pdf




How To Plot Z 5 Sqrt X 2 Y 2 0 Le Z Le 5 In Mathematica Mathematics Stack Exchange



1



What Is The Equation Of Sphere Passing Through The Circle X 2 Y 2 Z 2 2x 3y 4z 6 0 And 3x 4y 5z 15 0 And Cuts The Sphere X 2 Y 2 Z 2 2x 4y 6z 11 0 Quora



Http Www Math Drexel Edu Classes Calculus Resources Math0hw Homework11 7 Ans Pdf



Find The Area Of The Portion Of The Surface Of The Sphere X 2 Y 2 Z 2 4x That Is Cut Off By A Nappe Of The Cone Y 2 Z 2 X 2 Mathematics Stack Exchange




Find The Volume Of The Given Solid Bounded By The Cylinder Y 2 Z 2 4 And The Planes X 2y X 0 Z 0 In The First Octant Homework Help And Answers Slader



Http Math Ucdenver Edu Billups Courses Ma2423 Midterm Solutions Pdf




C Aporte



Http Mathweb Math Ncu Edu Tw Calc 98s Assist Hw 98s Hw9 Pdf



2



35 Reduce The Equation X 2 Y 2 Z 2 4x 2y 2z 4 0 To One Of The Standard Forms Classify The Surface And Sketch It Toughstem




Evaluate The Triple Integral 3z Dv Where E Is Bounded By The Cylinder Y 2 Z 2 9 And The Planes Study Com




Find The Points On The Cone Z 2 X 2 Y 2 Tat Are Closest To The Point 4 2 0 Youtube




Graphing 3d Graphing X 2 Y 2 Z 2 Intro To Graphing 3d Youtube



If U 2 1 X 2 Y 2 Z 2 Then Show That 2u X 2 2u Y 2 2u Z 2 0 Sarthaks Econnect Largest Online Education Community




Urgent Sin 1x Sin 1y Sin 1z I Prove Thatx 2 Y 2 Z 2 2yz Square Root 1 X 2 0 Please Answer In A Simple And Understanding Way Maths Inverse Trigonometric Functions Meritnation Com



C5
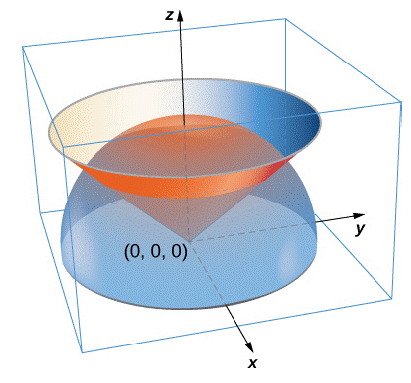



A Lamina Has The Shape Of A Portion Of Sphere X 2 Y 2 Z 2 A 2 That Lies Within Cone Z X 2 Y 2




6 Consider The Sphere S Cut Out By Z2 Y2 22 Maximize Daf P Where Y Z 2y 3z And U Is A Unit Vector In The Tangent Plane To S At



11 1 Introduction To Cartesian Coordinates In Space Chapter 11 Vectors Part Calculus Iii




Solved Verify That The Function U 1 Sqrt X 2



Http Ougouag Com 12 6exo Pdf




Vector Analysis By Alimkanwalimtinaa Issuu
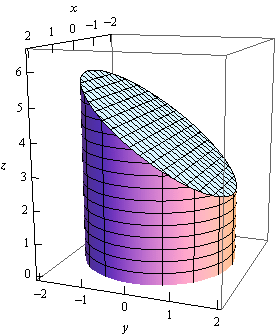



Calculus Iii Surface Integrals




Unit 2




Taller De Calculo Geometria Diferencial Formas Geometricas




Vector Analysis By Alimkanwalimtinaa Issuu




Sphere 3x 2 3y 2 3z 2 6x 12y 6z 2 0 Has Centre



Http Www Math Drexel Edu Classes Calculus Resources Math0hw Homework11 7 Ans Pdf




The Plane X 2y Z 4 Cuts The Sphere X 2 Y 2 Z 2 X Z 2 0 In A Ci




X Y Z 2 Y Z X 2 Z X Y 2 0 Then Find X Y Z Brainly In




X 2 Y 2 Z 2 0 Graph Dawonaldson
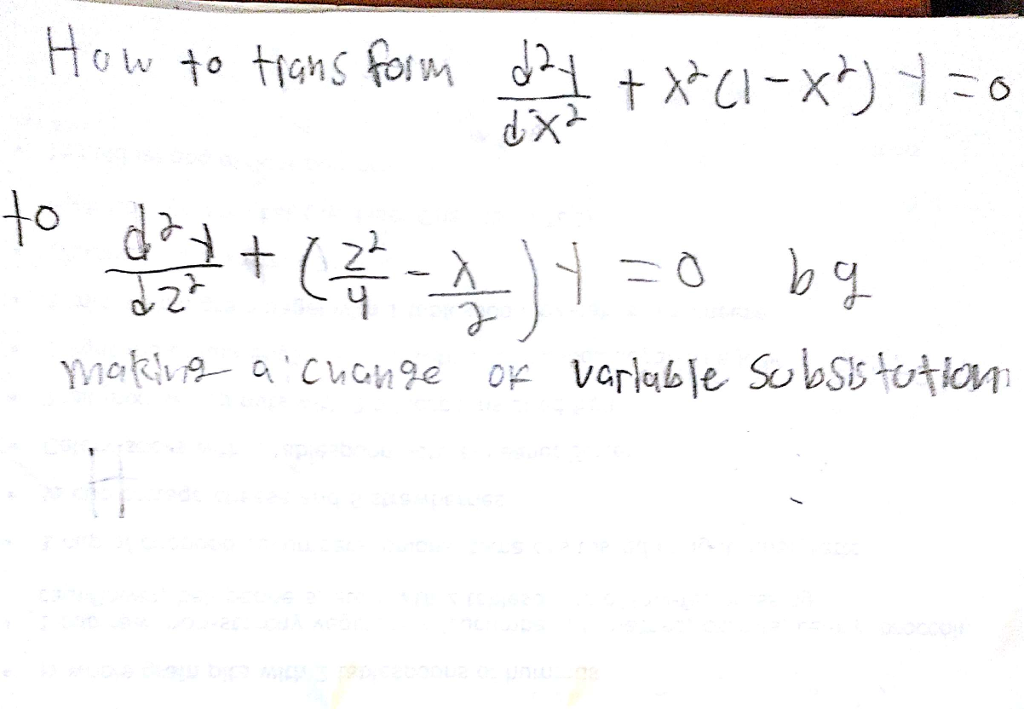



Solved Transform Differential Equation D 2y Dx 2 Lambda 2 1 X 2 Y 0 D 2y Dz 2 Z 2 4 Lamda 2 0 Q




Solutions For Review Problems
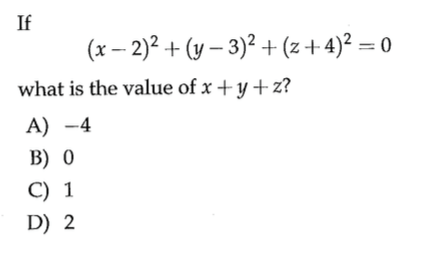



Answered If X 2 2 Y 3 2 Z 4 2 0 What Is The Bartleby



X 2 Y 2 Z 2 0 In A 3d Graph Chegg Com
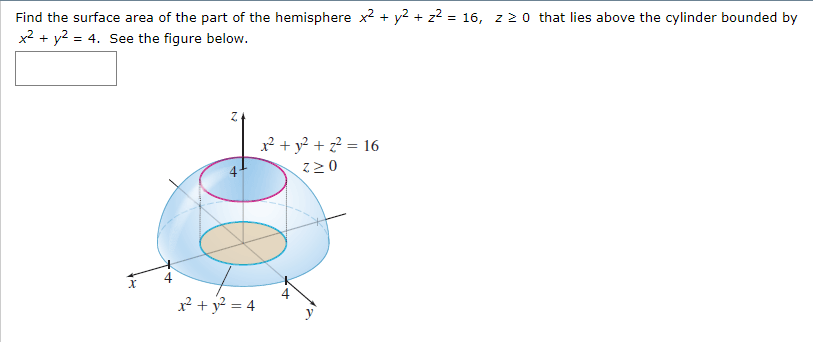



Find The Surface Area Of The Part Of The Hemisphere Chegg Com
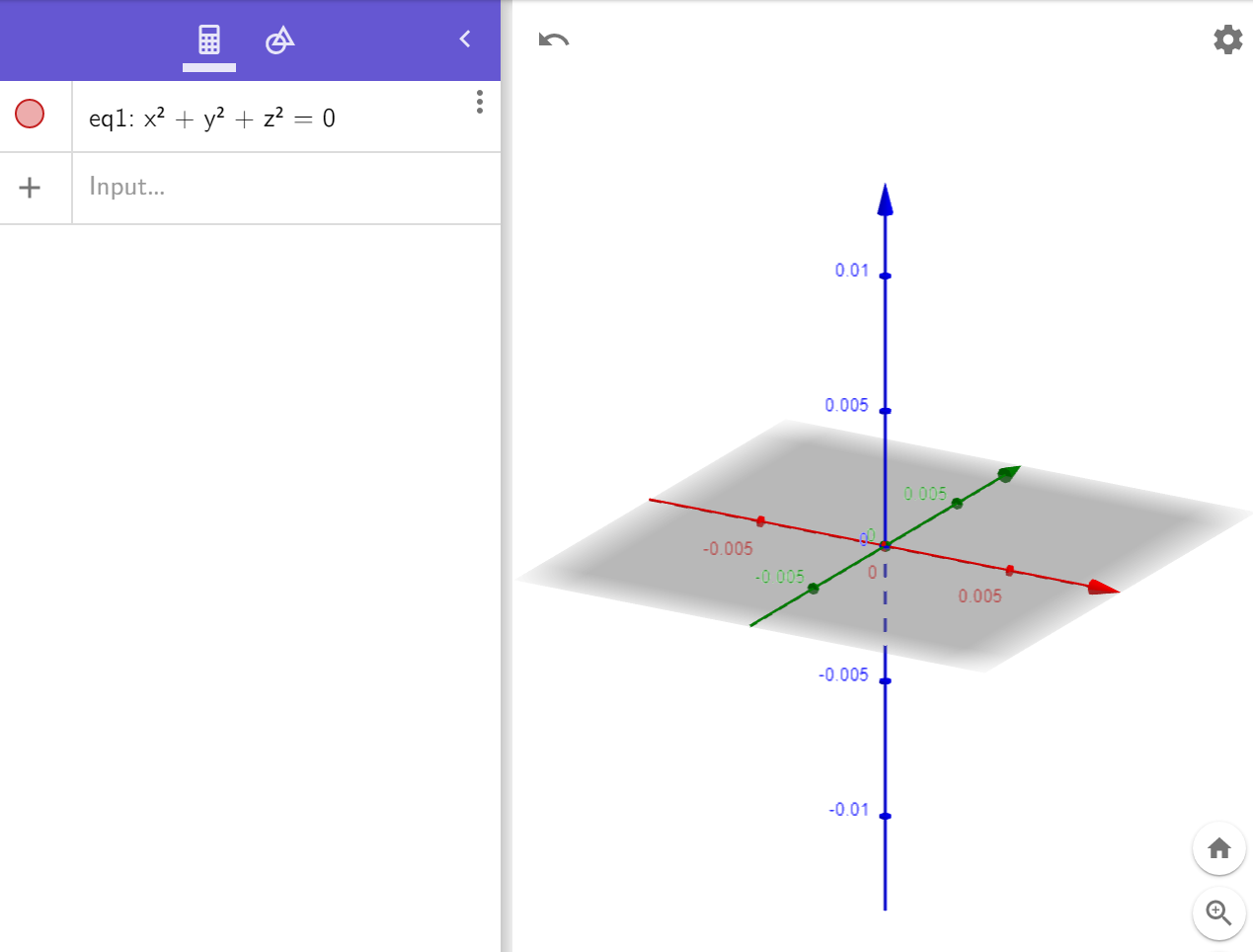



What Does The Equation X 2 Y 2 Z 2 0 Represent Chegg Com



Solved Form Partial Differential Equation By Eliminating The Arbitrary Function F Ax By Cz X 2 Y 2 Z 2 0 Also Find Order And Degree Of The Course Hero




Notes Up To Ch7 Sec3
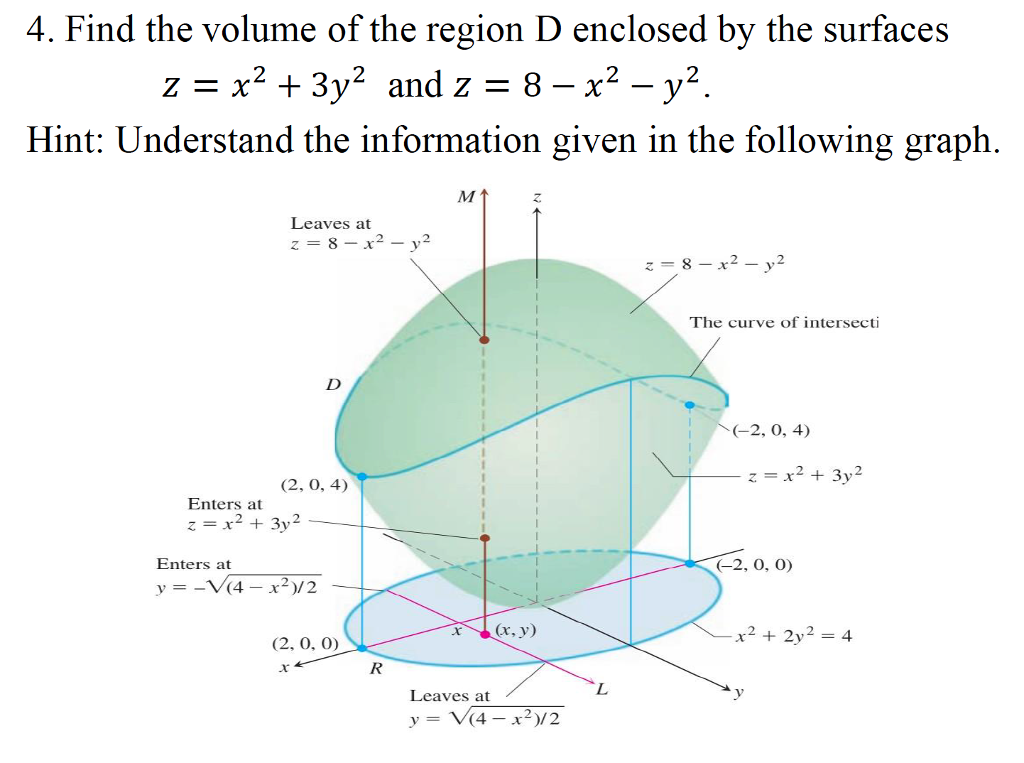



4 Find The Volume Of The Region D Enclosed By The Chegg Com



Surface Area




If X 3 2 Y 5 2 Z 4 2 0 Then Find X 2 9 Y 2 25 Z 2 16 Brainly In



Convert A Rectangular Equation To A Spherical Equation X 2 Y 2 Z 2 0 Youtube



Http Www Math Ntu Edu Tw Cheng Teaching Calculus Ch16 Pdf




Level Surfaces




If X Y Z 0 Then X 2 X Y Y 2 Equals Y 2 Y Z Z 2 B Y 2 Y




15 5 Triple Integrals In Cylindrical And Spherical Coordinates Mathematics Libretexts



1



Surfaces




The Lines X 1 2 Y 1 Z 2 And X Y Z 2 0 Lambdax 3z 5 Are Copla



Solved Form Partial Differential Equation By Eliminating The Arbitrary Function F Ax By Cz X 2 Y 2 Z 2 0 Also Find Order And Degree Of The Course Hero



35 Reduce The Equation X 2 Y 2 Z 2 4x 2y 2z 4 0 To One Of The Standard Forms Classify The Surface And Sketch It Toughstem




Find The Radical Centre Of Th See How To Solve It At Qanda



Answered Find The Points On The Cone Z2 X2 Bartleby
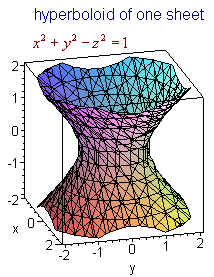



Surfaces



The Divergence Theorem Page 2




Describe The Given Set In Spherical Coordinatees 47 Chegg Com
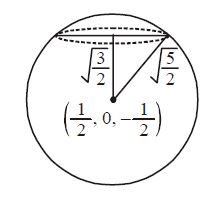



The Plane X 2y Z 4 Cuts The Sphere X2 Y2 Z2 X




The Equation Of The Plane Through The Intersection Of The Planes 3x Y 2z 4 0 And X Y Z 2 0 And The Point 2 2 1 Is
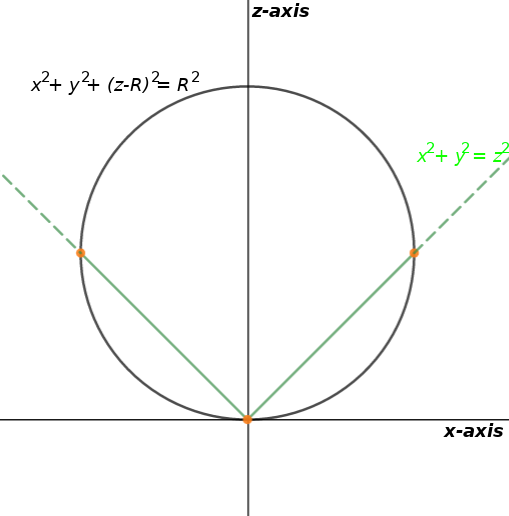



A Compute The Area Of The Portion Of The Cone Math X 2 Y 2 Z 2 Math With Math Z Geq 0 Math That Is Inside The Sphere Math X 2 Y 2 Z 2 2rz Math Where




Solved 8 Let S X Y Z E R X2 Y2 Z2 1 And H X Y Chegg Com
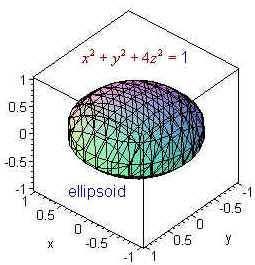



Surfaces




If X2 Y2 Z2 Xy Yz Xx O Prove That X Y Z Maths Polynomials Meritnation Com



Privado Results




By Transforming To Cylindrical Polar Coordinates Evaluate The Integral I Ln X 2 Y 2 Dxdydz Over The Interior Of The Conical Region X 2 Y 2 Z 2 0 Z 1 Holooly Com




Surfaces Part 2




7 4e Exercises Mathematics Libretexts


